Die Coronakrise hat ein grelles Licht auf die Grenzen der herkömmlichen Risikomodelle geworfen. Angesichts der Häufigkeit markanter Marktrückgänge, bei denen Aktien um 20 Prozent oder mehr fallen, sollte man meinen, dass Anlageexperten Renditeverteilungsmodelle verwenden würden, die derartige Rückschläge (und die nachfolgenden Erholungen) berücksichtigen. Aber leider beziehen viele gerade die Gefahr von Extremereignissen nicht in ihre Anlageentscheidungen ein.
Einige Investoren neigen dazu, Tools wie Portfolio-Optimierer und Monte-Carlo-Finanzplanungsmodelle zu verwenden, die sich auf so genannte Thin-Tail-Modelle stützen. „Thin Tails“ beziehen sich auf die Enden einer Verteilungskurve; sie in vielen Modellen flach, was auf eine geringe Wahrscheinlichkeit von Extremereignissen hinweist; Wahrscheinlichkeiten, die gering sind, werden in der Realität von vielen Investoren ignoriert oder übersehen. Mit schwerwiegenden Folgen.
In klassische Renditeverteilungsmodelle, die wiederum die Grundlage von Risikomanagement-Modellen sind, fließt die Annahme ein, dass schwere Marktkrisen sehr seltene Ereignisse sind. Doch ein Blick auf historische Ertragsdaten zeigt immer wieder, dass diese Krisen alles andere als selten sind. Daher möchte ich einen genaueren Blick auf zwei grundverschiedene Risikomodelle werfen und mögliche Schlussfolgerungen für Investoren ziehen.
Wie Modelle Renditen im Vergleich realen Renditen verteilen
Um zu sehen, wie die verschiedenen Verteilungsmodelle im Vergleich zueinander stehen, habe ich sie auf der Grundlage der monatlichen Marktrenditen in den USA von Januar 1886 bis März 2020 in der unten stehenden Grafik abgebildet. Das Diagramm enthält:
- eine lognormale Kurve, das dem Standardverteilungsmodell entspricht, das von den meisten Vermögensverwaltern verwendet wird und das vollständig auf der durchschnittlichen Marktrendite und der Standardabweichung der Rendite basiert;
- eine log-stabile Kurve, die eine Alternative zum Standardmodell darstellt, und
- eine auf realen historischen Ertragsdaten basierende Kurve, die sich nicht auf ein vordefiniertes Modell stützt
Grafik: Rendite-Modelle versus reale Renditen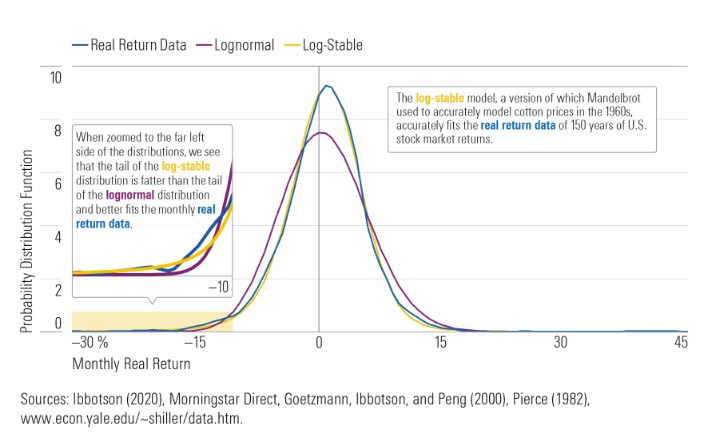
Aus dem Diagramm lässt sich Folgendes ablesen:
- Die lognormale Kurve ähnelt einer Glockenkurve. Diese Kurve hat flache Enden, was bedeutet, dass sie extremen Renditen, seien sie positiv oder negativ, praktisch keine Wahrscheinlichkeit beimisst.
- Die als „reale Ertragsdaten“ bezeichnete Kurve hat dickere Verteilungsenden als die Lognormal-Kurve, insbesondere auf der linken Seite. Das weist auf das oben angesprochene Problem hin, auf die höhere Häufigkeit extremer Negativ-Ereignisse). Auf der rechten Seite hat der Extremwert von etwa 40 Prozent ebenfalls ein gewisses Gewicht, was darauf hinweist, dass extreme Ereignisse in Summe häufiger auftreten, als es die Standardmodelle vorhersagen.
- Die als „log-stabil“ bezeichnete Kurve stimmt fast mit den tatsächlichen Ertragsdaten überein, mit einer hohen Spitze in der Nähe des mittleren und dickere Verteilungen an beiden Enden, was auf eine höhere Wahrscheinlichkeit sowohl extrem positiver als auch extrem negativer Erträge hinweist. Der vergrößerte Ausschnitt von der linken Seite der Verteilung zeigt, wie gut die log-stabile Verteilung mit dem „Fat Tail“ der realdaten-basierten Verteilung übereinstimmt.
Die Preisfrage lautet also:
Warum hat sich das Modell der log-stabilen Verteilung nicht durchgesetzt?
Das logarithmisch stabile Verteilungsmodell basiert auf der stabilen Paret'schen Verteilung, die der Mathematiker Benoît Mandelbrot erstmals in den 1960er Jahren als Modell für Veränderungen von Asset Preisen vorgeschlagen hat. Ein Grund dafür, dass dieses Modell nicht weit verbreitet ist, liegt an der fast schon revolutionären Prämisse, wonach eine Zufallsvariable, die einer stabilen Paret'schen Verteilung folgt, eine unendliche Varianz aufweist.
Die Annahme dieser Prämisse, dass die Varianz von Renditen unendlich sein kann, würde bedeuten, dass Markowitz' Mittelwert-Varianz-Modell der Portfoliokonstruktion ungültig ist. Das gilt auch für das Capital Asset Pricing Modell und die Arbitrage Pricing-Theorie. Mit anderen Worten: Die Annahme des logarithmisch stabilen Renditemodells würde bedeuten, dass fast die gesamte Standard-Finanzökonomie gekippt würde.
Der Finanzökonom Paul H. Cootner schrieb 1964 in seinem Buch „The Random Character of Stock Market Prices“ (Der Zufallscharakter von Börsenpreisen) über diese Implikation: „Bevor wir jahrhundertelange Arbeit auf den Aschehaufen werfen, möchten wir sicher sein, dass all unsere Arbeit wirklich nutzlos ist.“ An diesem Einwand hat sich im Prinzip bis heute nichts geändert, auch wenn seitdem mehrfach Extremereignisse stattgefunden haben.
Wie das log-stabile Verteilungsmodell weltweit Gestalt annimmt
Wir können die beiden Formparameter des stabilen paretischen Modells – peakedness (Spitzenwertparameter) und skewness (Schiefe) - bewerten, um zu zeigen, wie es sich auf die Renditen auswirkt und wie das lognormale Modell zu kurz greift.
- Der Spitzenwertparameter gibt an, ob eine Verteilung eine endliche oder unendliche Varianz hat und wie weit sich die dickeren Verteilungsenden auf beiden Seiten ausdehnen. Ein Spitzenwertparameter kann zwischen 0 und 2 fallen, wobei ein Parameter von 2 eine Normalverteilung und endliche Varianz anzeigt. Ein Parameter von weniger als 2 signalisiert unendliche Varianz; je weiter der Wert unter 2 liegt, desto höher die Mitte und desto dicker die Enden. Das heißt: je stärker der Wert unter 2 liegt, desto größer ist die Wahrscheinlichkeit von Extremereignissen.
- Der Parameter Schiefe gibt die Asymmetrie der Verteilung an. Der Schiefe-Parameter liegt zwischen negativ 1 und positiv 1, wobei ein Wert von 0 bedeutet, dass die Verteilung symmetrisch ist. Ein negativer Wert bedeutet, dass die Verteilung nach links geneigt ist (was bedeutet, dass extreme negative Ereignisse wahrscheinlicher sind als extreme positive Ereignisse); ein positiver Wert bedeutet, dass die Verteilung sie nach rechts geneigt ist, was bedeutet, dass extrem positive Ereignisse wahrscheinlicher sind als extrem negative Ereignisse.
Um zu sehen, wie gut das log-stabile Modell in Einklang mit den Aktien-Renditen weltweit funktioniert, habe ich es an die monatlichen Renditen der Morningstar-Börsenindizes für 33 Länder von Juli 1998 bis Februar 2020 angepasst. Diese Ergebnisse sind in der nachstehenden Grafik als Streudiagramm der Parameter Schiefe und Spitzenwert dargestellt.
Grafik: Peakedness und Skewness Parameter für 33 Morningstar-Länderindizes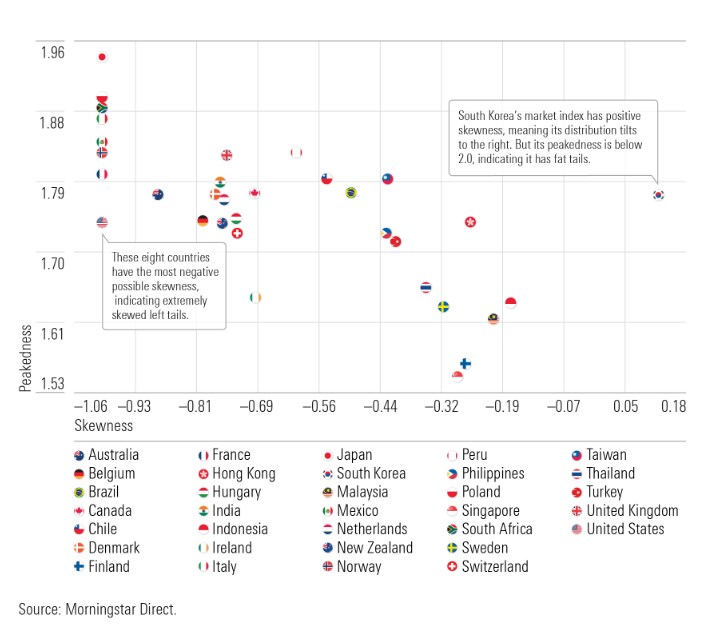
Wie aus der oberen Grafik hervorgeht, liegt der Spitzenwert-Parameter für alle Länder unter 2, was darauf hinweist, dass die Renditen aller Länder Extremereignisse erfahren haben. Für den Skewness-Parameter ergaben alle Länder mit Ausnahme Südkoreas einen negativen Wert. Acht Länder (Frankreich, Japan, Italien, Südafrika, USA, Mexiko, Norwegen und Polen) hatten Schiefe-Parameter von minus 1, dem negativsten möglichen Wert, während alle anderen zwischen 0 und minus 1 fielen, was heißt, dass alle diese Länder extreme negative Ereignisse erlebten.
Diese Analyse zeigt, dass extreme Ereignisse ein weltweit auftretendes Phänomen sind. Diese Abweichung von dem, was Standardrisikomodelle vorhersagen, legt nahe, dass Mandelbrots Arbeit über die Verteilung von Preisänderungen von Praktikern mehr Aufmerksamkeit geschenkt werden sollte.
Verteilungsmodelle brauchen eine realistische Sicht auf Risiken
Extreme Ereignisse finden sich in den historischen Aktienrenditen an allen Märkten der Welt. Dennoch existieren diese Extremereignisse in den statistischen Standardmodellen der Finanzwirtschaft nicht. Auch wenn das ein Manko ist, sollten Anleger indes nicht das Kind mit dem Bade ausschütten und die üblichen Methoden zur Messung von Renditen und Risiken über Bord werfen. Vielmehr sollten sie sowohl die Grenzen der Standardrisikomodelle als auch das Potenzial des log-stabilen Modells verstehen.
Für eine vollständigere Bewertung der Risiken von Aktieninvestitionen sollten Investoren drei Schlüsselfragen stellen:
- Wie wahrscheinlich ist eine Korrektur?
- Wie lange könnte sie andauern?
- Wie schlimm könnte sie werden?
Abschwünge sind zahlreich und können lang und schmerzhaft sein. Anleger, die auf diese Ereignisse vorbereitet sind, werden sich wappnen und Krisen besser überstehen als Investoren, die nichtsahnend in Krisen hineinstolpern. Anleger, die auf Extremes vorbereitet sind, dürften auch besser positioniert sein, um von der unvermeidlichen nachfolgenden Erholung zu profitieren.
Verpassen Sie nichts. Alle Morningstar Analysen können Sie in unseren wöchentlichen Newslettern gratis mitbekommen. Hier anmelden und immer auf dem Laufenden bleiben.